LSA
LSA即潜语义分析(或主题模型,主题即为潜在的语义信息),认为“一篇文章是通过一定的概率选择了某个主题,并从这个主题中以一定概率选择某个词语”这样一个过程得到的。
目标是:通过对“文档-单词”矩阵进行分解,得到“文档-主题”和“主题-单词”两个概率分布,即根据给定的一篇文档,推测其主题分布。
主要有2种主要方法:奇异值分解SVD、非负矩阵分解NMF。
单词集合W={w1, w2, …, wm}
文档集合D={d1, d2, …, dn}
单词向量空间Xm*n:单词-文本矩阵,每个单词在文档中出现的频率(行-单词,列-文档)
话题向量空间Tm*k:单词-话题矩阵,每个单词在话题中出现的频率(行-单词,列-话题),T是X的一个子集
文本在话题空间的向量表示Yk*n: Xmn = Tmk * Ykn,Ykn 就是我们需要求得的隐变量,即每个文本对应每个话题的权重,可将每个文本标记为权重较大的话题上。
[截断] 奇异值分解(SVD)
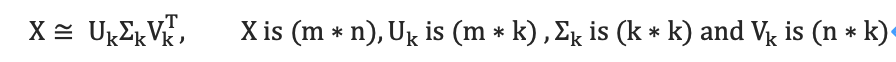
因此,话题向量空间是 ,文本在话题空间的表示是 ,k为主题的数目(提前设定主题数目k,即截断SVD)。
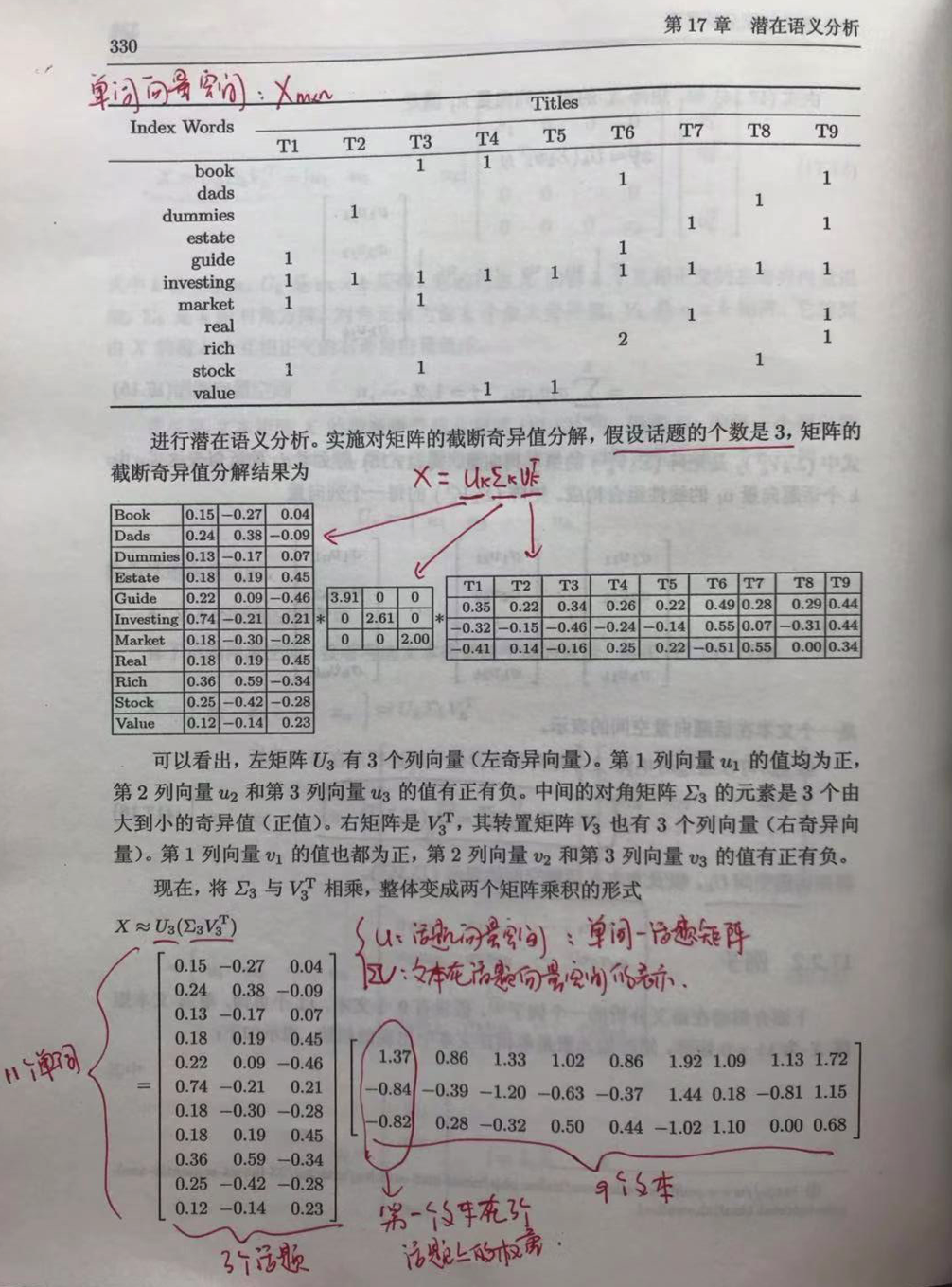
非负矩阵分解(NMF)
若一个矩阵的所有元素均为非负,则为非负矩阵。对于一个非负矩阵Xmn,可以找到两个非负矩阵Wmk和Hkn,使得:
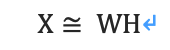
因此,话题向量空间是W,文本在话题空间的表示是H,k为主题的数目。
LSA的推荐应用
此时的隐语义,即通过用户-商品矩阵进行分解,得到的潜在用户兴趣。就是根据用户的当前偏好信息,得到用户的兴趣偏好,将该类兴趣对应的物品推荐给当前用户。
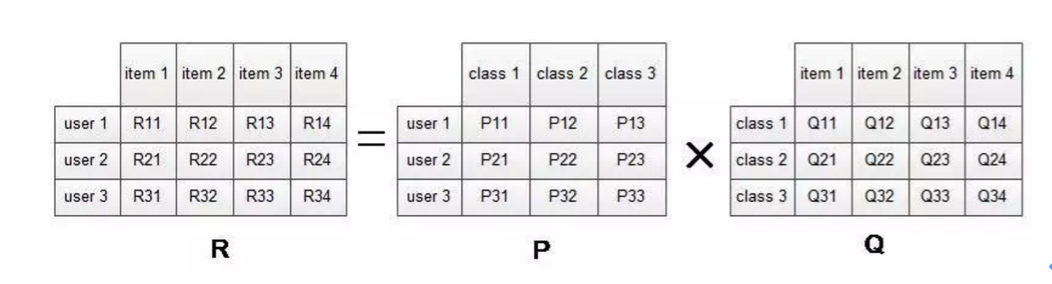
缺点:隐语义模型训练耗时,不能因为用户行为的变化实时地调整推荐结果,来满足用户最近的行为。
pLSA
Probabilistic Latent Semantic Analysis, pLSA,基于概率的隐性语义分析。
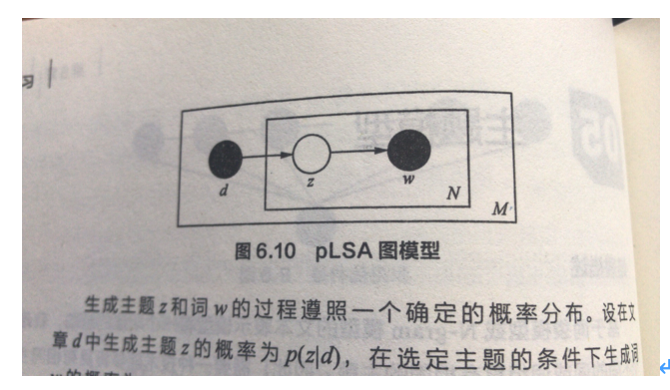
思想:单词已一定概率生成主题(单词分布p(w|z)),主题已一定概率生成文档(主题分布p(z|d)),因此在已知文档(d)和单词(w)的情况下,估计主题(z,即隐变量),由EM算法介绍可知,在含有隐变量时,使用EM算法求的概率模型的最优参数,即p(w|z)和p(z|d)。
其中,D代表文档,Z代表隐含主题,W代表观察到的词,P(d)表示选中文档d的概率,P(z|d)表示给定文档d中主题z的概率,P(w|z)表示给定主题z、出现单词w的概率,P(d,w)表示文档d与单词w联合出现的概率,为唯一的已知概率。
此外,pLSA使用EM估计参数,并且估计的参数是固定的(概率思想)。
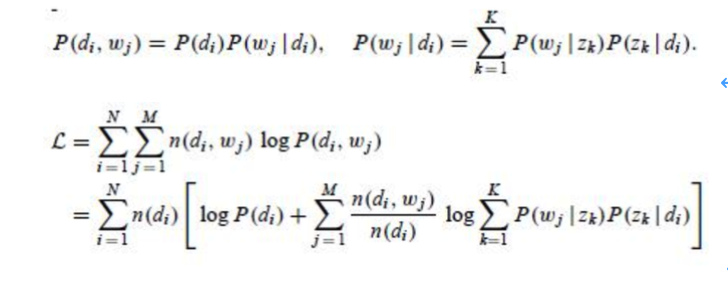
LDA
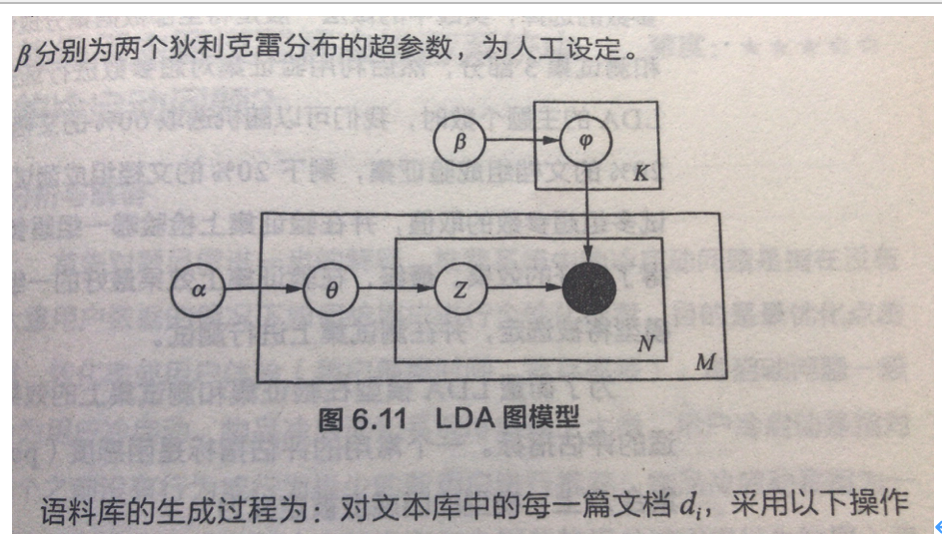
Latent Dirichlet Allocation,LDA,基于贝叶斯。
与pLSA不同的是,pLSA中认为P(z|d)和P(w|z)看成是确定的未知常数,并可以求解出来;而LDA认为待估计参数不再是一个固定的常数,而是服从狄利克雷分布的随机变量,
该随机变量通过2个Dirichlet先验参数生成的。
参考: