极大似然算法
极大似然算法的思想:知道结果,反推条件θ
如果概率模型不依赖隐变量,则可直接用极大似然算法获取参数估计值。
举例:随机抛硬币A和B很多轮,每轮记录A和B是正面还是反面的次数,估计A正面朝上的概率、B正面朝上的概率。
求极大似然函数估计值的一般步骤
a) 写出似然函数;
b) 对似然函数取对数,并整理;
c) 求导数,令导数为0,得到似然方程;
d) 解似然方程,得到的参数即为所求;
e) 如果是n个参数,则计算每个参数的偏导数=0,最后解n方程组,就是似然函数的极值点了。
对数似然函数
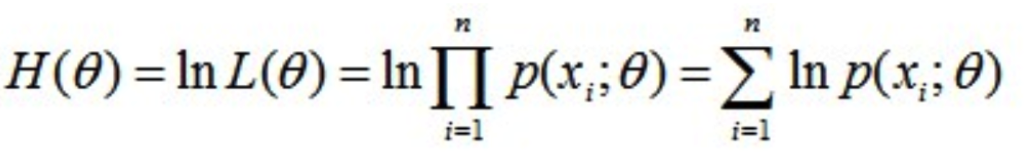
EM算法
最大期望算法(Expectation-maximization algorithm,EM),是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。
隐变量
EM算法与极大似然算法的区别是,EM算法中包含隐变量。
举例:随机抛硬币A和B很多轮,每轮不知道当前抛的是A硬币还是B硬币(即隐性变量),记录正面还是反面的次数,然后估计A正面朝上的概率、B正面朝上的概率。由于其中包含隐变量,已知隐变量时,则转化为极大似然算法,而未知隐变量时,则采取EM算法。
EM的2个步骤
第一步是计算期望(E),先参数初始化,而后计算隐藏变量的当前估计值;
第二步是最大化(M),基于E步骤的隐变量估计值,计算似然函数的最大似然值,获取新的参数估计值。
M步上找到的新的参数估计值,被用于下一个E步计算中重新计算隐变量估计值,这个过程不断交替进行,直至参数不再变化,模型收敛。
参考: